この記事の内容
この記事では、Pythonにてサンプルデータを用いて、単回帰分析を行う方法を紹介します。例として、広告費から売上を求めてみます。
この記事を読むことで、以下を学ぶことができます。
- 単回帰分析の基礎
- Pythonを使用して単回帰分析ロジックの実装方法
概要
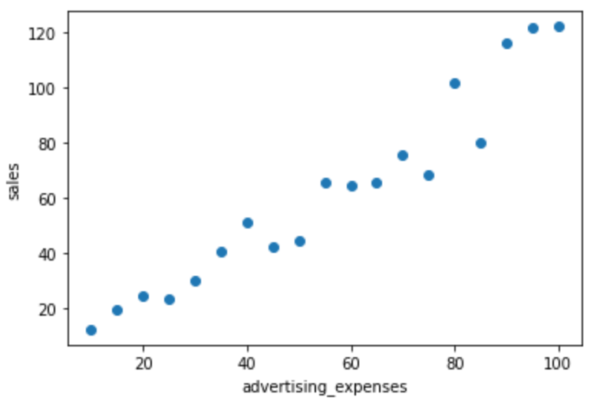
以下の、広告費(advertising_expenses)と売上(sales)が記載されたデータを使用して、単回帰分析を行います。
X軸が広告費、Y軸が売上になります。
今回の目的は単回帰分析を用いて、「広告費をどれだけかけると、どの程度の売上になるのか予測する」ことです。この方法を用いることで、1変数(この場合、広告費)から、予測値を求めることができるようになります。
多変数を扱う場合は、重回帰分析を行うことになりますが、今回は対象外とします。
今回の単回帰分析が有効であるかどうかは、まずデータが一次関数(y=ax + b)に近い形でないと、予測値が外れてしまうので、注意が必要です。
使用するデータ
今回使用するサンプルデータは、以下よりダウンロードが可能です。
単回帰分析の基礎
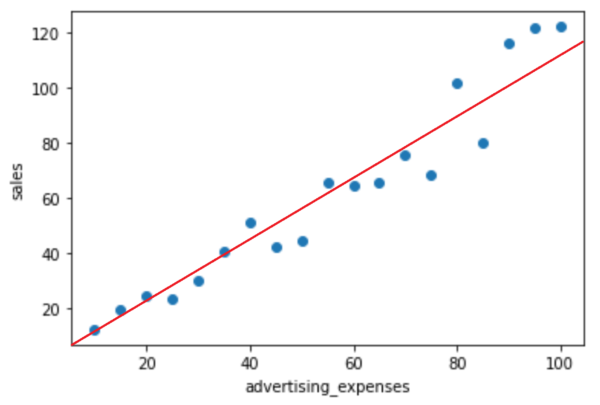
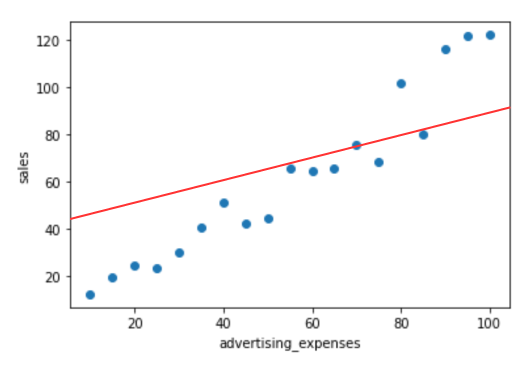
広告費から、売上を予測できるようにするためには、式 y = ax + bで、実データによりフィットするaとbを求める必要があります。これらを求めることで、以下のような赤線を引く関数を導くことができます。これにより、広告費から、おおよその売上を求めることができます。
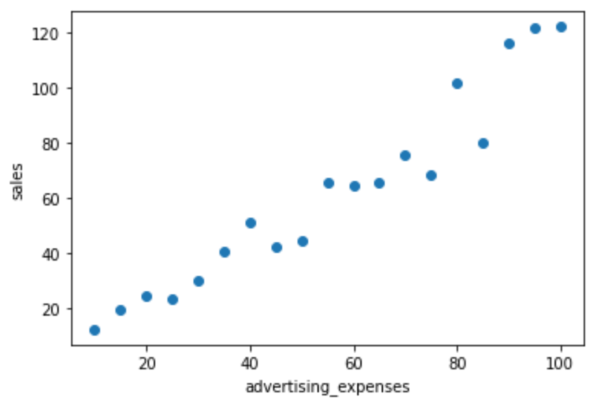
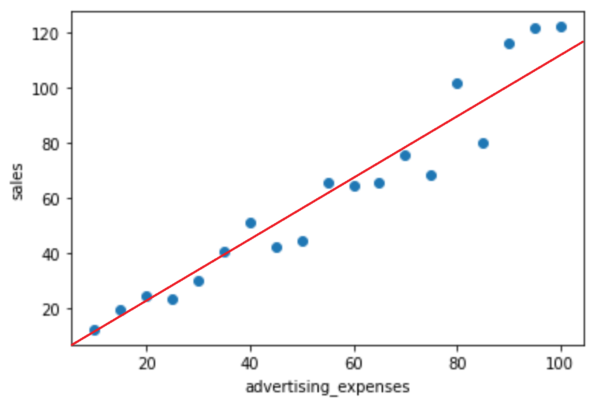
では、よりフィットするパラメータがどういうものなのか考えてみましょう。以下の2つの図を見比べると、前者の方がよりフィットしている曲線といえ、後者はあまりフィットしていない関数といえると思います。この違いは、予測線と各実際の値との乖離の大きいか少ないにかかわってきます。
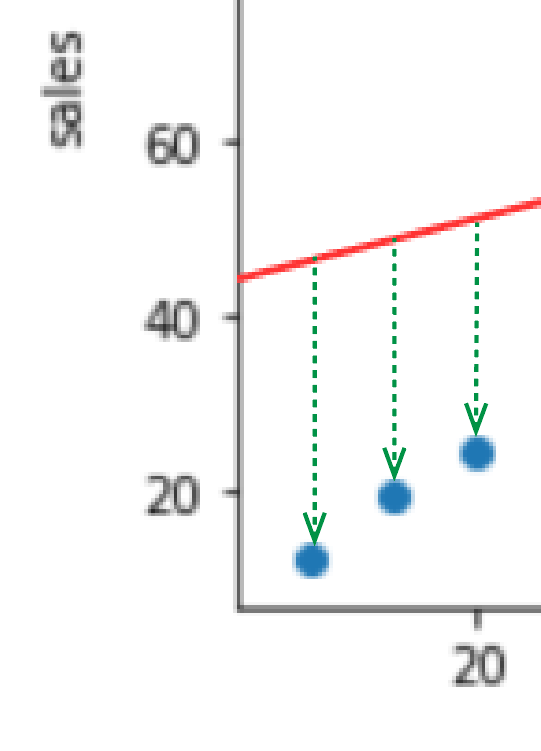
例えば、後者の図の一部を見てみると、予測線と、実際の値はこのように乖離していることがわかります。前者の図ではこのように大きく乖離している部分は後者と比べ少ないです。
そのため、より良い関数を求めるには、予測線との誤差を極力減らしてあげることが重要になります。そのための方法を後述していきます。
データの中心化を行う
パラメータのaとbを求めることが最終目的です。しかし、ここでは、簡易に求めることができるようにするために、データの中心化を前処理として行うこととします。この中心化を行うことで、パラメータのbを求める必要がなくなります。どういうことかというと、実際のデータを中心化(切片を0に)することで、以下の式とすることができます。
$$
\hat{y}=ax\\
\hat{y} : 予測値
$$そのために、x値及びy値をそれぞれ実際のデータの平均値を引くことで中心化することができます。
$$
xc=x-\bar{x}\\
yc=y-\bar{y}\\
xc : 中心化したxの値\\
yc : 中心化したyの値\\
$$
こうすることで、データを中心化することができ、切片を考えずに単回帰分析の式を求めることができます。
損失関数を求める
予測する線と実際の値の誤差がより少ない場合、良いパラメータといえます。それを評価するための関数を損失関数と呼びます。損失関数の値が小さければ小さいほど良いパラメータといえます。損失関数は以下の定義となります。
$${\cal L} = \sum_{n=1}^{N}(y_{n}-\hat{y_{n}})^2\\
{\cal L}:損失関数\\
y_{n} : 実データ\\
\hat{y_{n}} : 予測値\\
$$
実際の値から予測値を引いたものを二乗したものを足し合わせる形になります。二乗しているのは、予測値からのずれを考慮したいため、符号を気にしないようにしたいためです。上にずれても、下にずれても同一の符号(プラス)で扱いたいためです。
損失関数を最小化する
損失関数の傾きが0になる場合のaを偏微分して求めます。式は以下の通りです。
$$\frac{\partial}{\partial a}({\cal L}) = 0$$
損失関数は、以下となります。
$${\cal L} = \sum_{n=1}^{N}(y_{n}-ax_{n})^2$$
損失関数を展開します。
$${\cal L} = \sum_{n=1}^{N}(y_{n}^{2}-2y_{n}ax_{n}+a^{2}x^{2}_{n})$$
aで偏微分していきます。
$$\frac{\partial}{\partial a}(\sum_{n=1}^{N}(y_{n}^{2}-2y_{n}ax_{n}+a^{2}x^{2}_{n})) = 0$$
$$={\sum_{n=1}^{N}}(-2x_{n}y_{n}) + \sum_{n=1}^{N}(-2ax^{2}_{n}) = 0$$
aを求めたいので、a = の式に変形します。
$$
a = \frac{\displaystyle{\sum_{n=1}^{N}}x_{n}y_{n}}{\displaystyle{\sum_{n=1}^{N}}x_{n}^{2}}
$$
以上の式が、傾き0のaを求める式になります。次は、実際にPythonでプログラミングを行います。
Pythonで実際に実行してみる
今回はnumpy, pandas, matplotlibを使用していきますので、以下をインポートします。
import numpy as np import matplotlib.pyplot as plt import pandas as pd
次にpandasで、csvをデータフレームに読み込みます。
df = pd.read_csv('sample_data.csv')
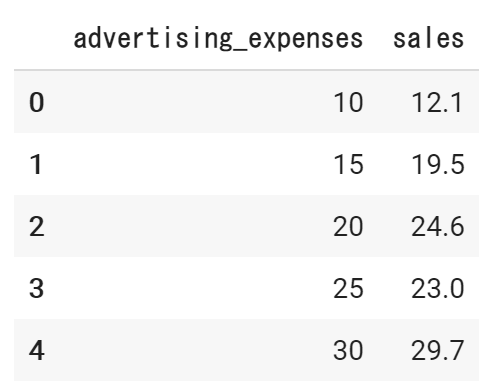
読み込んだ結果を一度確認してみます。
df.head()
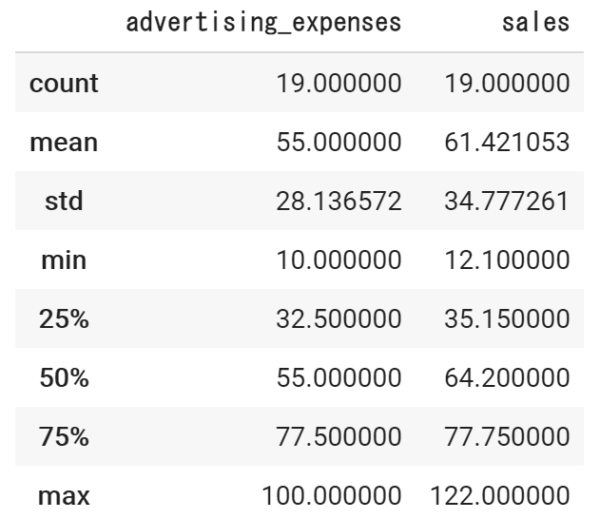
df.describe()
データをmatplotlibで可視化してみます。
plt.scatter(df['advertising_expenses'], df['sales'])
plt.xlabel('advertising_expenses')
plt.ylabel('sales')
plt.show()
データの中心化を行います。
df_c = df - df.mean()
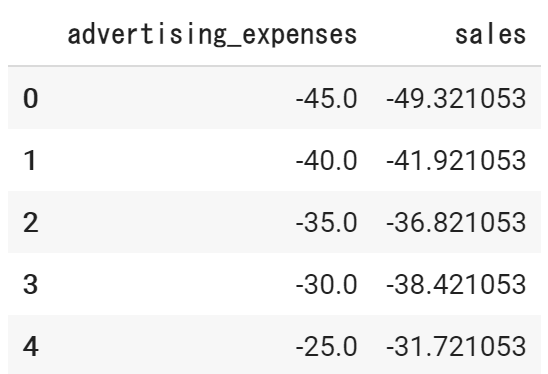
中心化したデータも同様に確認します。
df_c.head()
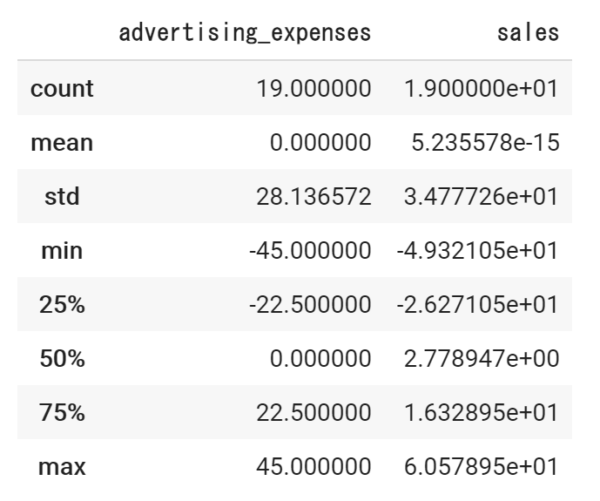
統計情報も確認します。中心化することで平均値(mean)が0となります。
df_c.describe()
※ salesのmeanが誤差で、5.235578e-15となっていますが、0.0000…52という値でほぼ0の値なので問題ありません。
aの値を求めます。式は以下の通りです。
$$
a = \frac{\displaystyle{\sum_{n=1}^{N}}x_{n}y_{n}}{\displaystyle{\sum_{n=1}^{N}}x_{n}^{2}}
$$
x = df_c['advertising_expenses'] xx = x * x y = df_c['sales'] xy = x * y a = xy.sum() / xx.sum() a # >> 1.192842105263158
aが導出されたので、予測線を表示してみます。
plt.scatter(df_c['advertising_expenses'], df_c['sales'])
plt.plot(x, a*x)
plt.xlabel('advertising_expenses')
plt.ylabel('sales')
plt.show()
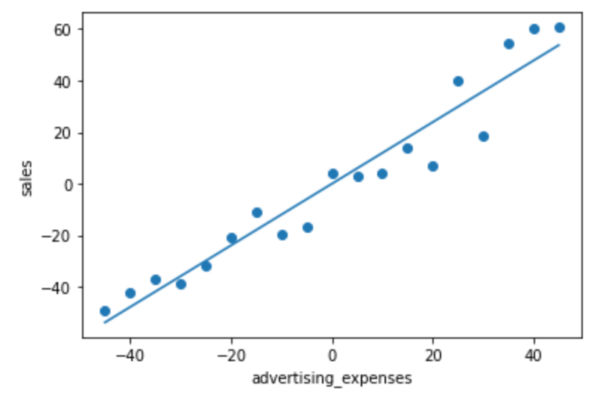
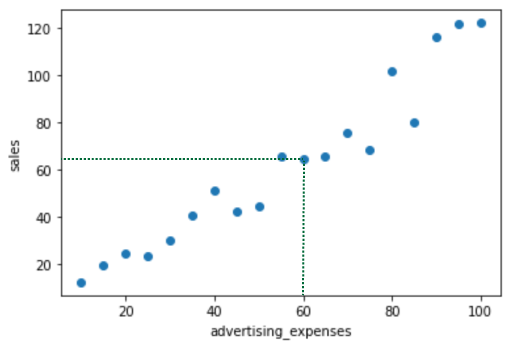
導出したaを使用して、試しに広告費が60の場合の売上を計算します。xに指定する値は、中心化する必要があるので、中心化した値を用います。また、y_hatにdf[‘sales’].mean()を加算しているのは、中心化した値を元のスケールに戻すためのものになります。予測値は67.38526315789474となりおおよそあっているといえるでしょう。
target_x = 60 - df['advertising_expenses'].mean() y_hat = target_x * a + df['sales'].mean() y_hat # >> 67.38526315789474
最後に
この記事では、単回帰分析の基礎および、Pythonでの実装方法について記載しました。
scikit-learn などのライブラリを用いることでより簡単に求めることができます。しかし、基礎を理解するためには数式から学んでおく必要があると思い、あえてライブラリは使っていませんでした。基礎を理解したのちに、ライブラリを用いて計算してみると良いかと思います。



コメント